@LoyFan
mathjax:true

在实数域中,连接两个真理的最短的路径是通过复数域 ——雅克·阿达马
复数认知阶段
阶段一
高中数学定义
再定义复数
这样一元二次方程就总是有解了!
然后就可以出很多乱七八糟的考题了!
阶段二
有了复数之后,以下原本在实数上不可以进行的操作都可以进行
- 任意开根号
- 对负数做对数运算
但这两种还是不可以
- 除以0
- $\log (0)$
扩展数系
问:扩展数系的时候,为什么不能发明一种数系,兼容“除以0”这个操作呢?
答:因为没有办法自洽,兼容“除以0”之后会得到悖论。所以“兼容除以0”这个目标就是错误的。就像“永动机”这个目标一样。
问:扩展数系的时候,为什么可以轻松得到$i=\sqrt{-1}$?
答:因为复数这个东西本来就是合理的,等待人们发现而已。(有一种轮回的感觉。。)
复数是二维的数
假设有一个生活在二维空间中的纸片人: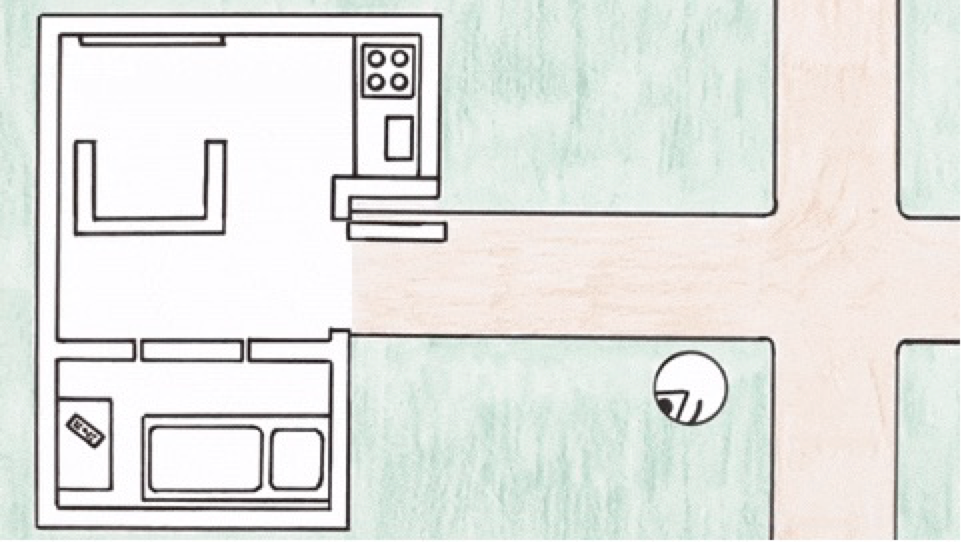
突然发现有一个黑点在草地上忽大忽小的闪烁,纸片人完全不知道怎么去解释: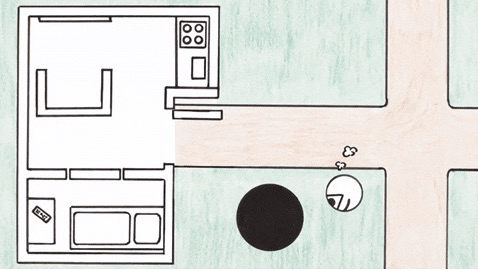
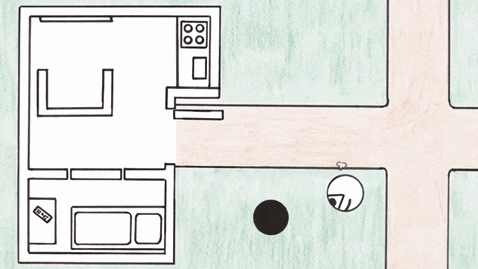
如果切换到三维视角去的话,问题就很简单了,原来是一个三维的球体穿过二维平面: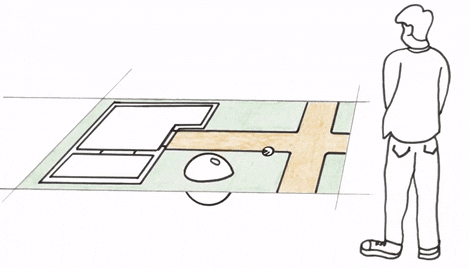
实数是一维的数,既生活在一维的实数轴上,又困囿其上:
而复数生活在二维复平面,拥有更大的自由度: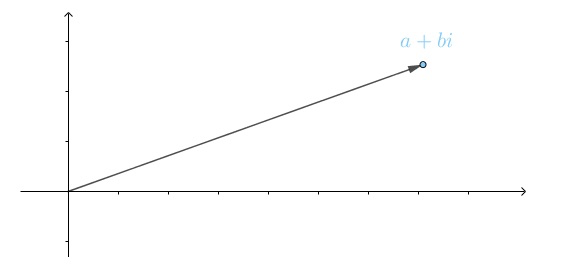
复数的历史
纸片人卡尔达诺
意大利数学家,吉罗拉莫·卡尔达诺(1501-1576),在它的著作《大术》中(这本书首次记载了一元三次方程的完整解法)提到这个一个问题,能否把10分成两部分,使它们的乘积为40?
他给出一个答案,令:
这样就满足题目的要求:
不过他自己也认为这不过就是一个数学游戏,虽然出现了虚数,但是“既不可捉摸又没有什么用处”。
此时的卡尔达诺就好像之前的纸片人,虽然想到了虚数,触摸到了更高的维度,但是终究还是把它看成一种幻想。
之后的笛卡尔把$i=\sqrt{-1}$称为虚数,也就是虚幻的、想像出来的数;莱布尼兹描述它为“介乎于存在与不存在之间的两栖数”。
确实,纸片人要跳出自己的维度去想问题是非常困难的。
邦贝利的思维飞跃
拉斐尔·邦贝利(1526-1572),文艺复兴时期欧洲著名的工程师,同时也是一个卓越的数学家,其出版于1572年的《代数学》一书讨论了负数的平方根(虚数):
正是这本书产生了一个思维飞跃。
标准的一元二次方程
在$b^{2}-4ac < 0$时曲线与x轴不相交,应该无解。
一元三次方程
通解是
假设方程
图像是
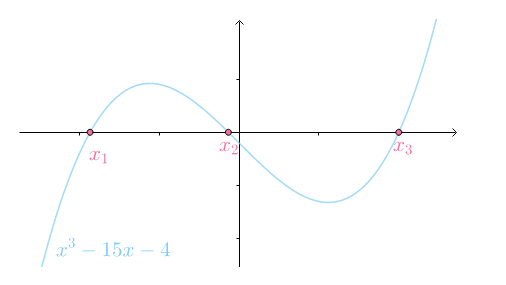
套用通解得到
邦贝利指出:从几何上看是有解的,但是必须通过虚数来求解!
邦贝利大胆地定义了复数的乘法(就是多项式乘法的合理延伸):
最终通过复数以及复数乘法,邦贝利解出了此方程的三个实数解。
这是一个巨大的思维飞跃,就好像刚才的纸片小人,困惑于“为什么有一个黑点在草地上忽大忽小的闪烁”?最终发现,需要通过更高纬度才能真正解决这个问题。邦贝利通过更高维度的复平面,解决了低维度的实数问题,真正的把复数带入了人们的视野。所以他被认为是复数的发现者。
更高维的数
自然会有这么一个问题,是否有更高维度的数?答案是有的,比如四元数。
威廉·哈密顿爵士(1805-1865)发现了四元数:
其中i、j、k就是对虚数维度的扩展。为此还成立了四元数推广委员会,提议学校像实数一样教授四元数。
四元数刚开始的时候引起了很大的争议,计算很复杂,但是用处不明显。用处不明显的原因或许是,当时面临的问题还不够复杂,还用不到比复数还高的维度。到了现代,终于在电脑动画中、量子物理中找到了四元数更多的应用,只是这些应用对普通人距离太远了。