Mar.9.2019
绪论
什么是机器学习?
- Arthur samuel 1959年创造了这个词 “Machine Learning”——Field of study that gives computers the ability to learn without being explicitly programmed.
“在没有明确设置的情况下,使计算机具有学习能力的研究领域。”
编写了跳棋程序,使机器自己与自己对弈,学会下棋。 - Tom Mitchell 1998 Well-posed Learning Problem:A computer program is said to learn from experience E with respect to some task T and some performance measure P,if its performance on T,as measured by P,improves with experience E.
“一个适当的学习问题定义如下:计算机程序从经验E中学习,解决某一个任务T,进行某一性能度量P,通过P测定在T上的表现因经验E而提高。”
Mar.10.2019
监督学习、无监督学习
- 监督学习(Supervised Learning):
我们给算法一个数据集,其中包含了数据对应的“正确答案”,算法的目的是找到更多正确答案。
- 连续值:也被称为“回归问题”:我们想要预测连续的数值输出。(房价和面积的例子)
- 离散值:分类问题、无穷多特征(肿瘤特征预测肿瘤良性恶性的例子)
- 无监督学习(Unsupervised Learning):
不提供“标准答案”,不给分类标准,要求找到数据集的结构,簇等。
- 聚类算法(clustering algorithms)比如谷歌的新闻分类。
- 鸡尾酒会算法:两个人同时说话,两个远近不同的麦克风同时记录,通过两个音频记录,无监督算法区分、分离出两个人的声音
算法代码:
[W,s,v] = svd((repmat(sum(x.x,1),size(x,1),1).x)*x’);
单变量线性回归
Mar.11.2019
模型描述

$\text { Hypothesis: } \quad h_{\theta}(x)=\theta_{0}+\theta_{1} x$
学习算法:根据训练集得到假设函数(Hypothesis)。
Mar.12.2019
代价函数
求线性假设函数的参数:代价函数(cost function),要求得使得代价函数最小的参数值。
代价函数最常用:平方误差函数
$\begin{array}{l}{\text { Hypothesis: }} \\ {h_{\theta}(x)=\theta_{0}+\theta_{1} x} \\ \\ {\text { Parameters: }} \\ {\theta_{0}, \theta_{1}}\end{array}$
$\begin{array}{l}{\text { cost Function: }} \\ {J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1 \diamond}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}}\end{array}$
$\begin{array}{l}{\text { Goal: minimize } J\left(\theta_{0}, \theta_{1}\right)}\end{array}$
梯度下降
求代价函数的参数的算法,通过每次改变参数值,直到收敛,找到局部最优解。
α:学习率(决定每一轮的参数的更新幅度),取值不能过小(太慢),取值不能过大(导致无法收敛converge甚至发散diverge)
线性回归的梯度下降
将平方误差代价函数用于梯度下降
Gradient descent algorithm
$\begin{array}{l} {\text { repeat until convergence } } \\ {\{} \\\\ {\theta_{0} :=\theta_{0}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)} \\ {\theta_{1} :=\theta_{1}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x^{(i)} } \\\\ {\}}\end{array}$
线性代数回顾
视频链接
内容程度大概是线性代数入门的两节课,可以略过。
配置
视频链接
根据自己的实验环境安装配置Octave和MATLAB
多变量线性回归
多功能
$\begin{array}{l}{\text { Hypothesis: } h_{\theta}(x)=\theta^{T} x=\theta_{0} x_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n}} \\ {\text { Parameters: } \theta_{0}, \theta_{1}, \ldots, \theta_{n}} \\ {\text { cost function: }} \\ {J\left(\theta_{0}, \theta_{1}, \ldots, \theta_{n}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}}\end{array}$
多元梯度下降法

Mar.13.2019
特征缩放
特征的取值范围差异很大的话,梯度下降算法的收敛速度非常缓慢。
需要将特征缩放到相近似的范围内,比如每个特征的值除以它的范围。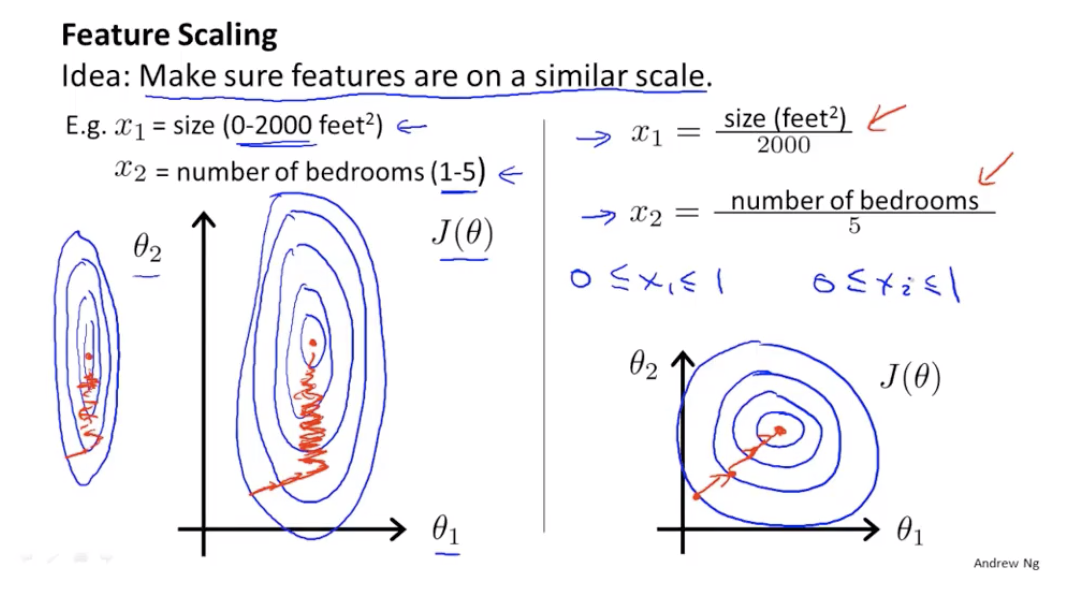


学习率的选取

Mar.15.2019
特征和多项式回归
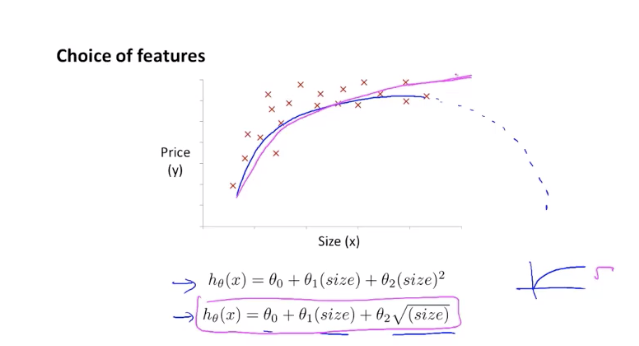
Mar.16.2019
正规方程法(非迭代)
计算使得代价函数最小的参数向量θ的算法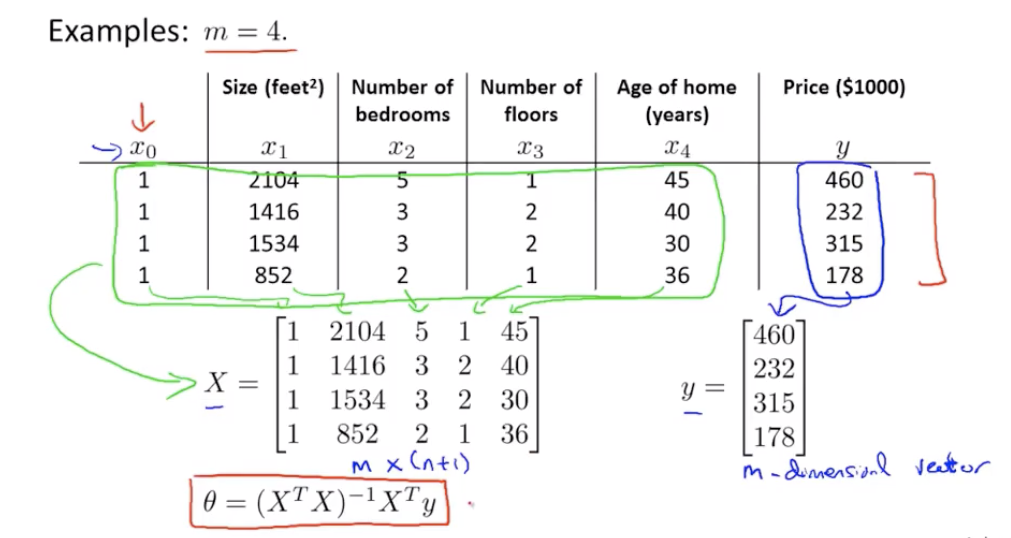
公式 $θ=(X^TX)^{-1}X^Ty$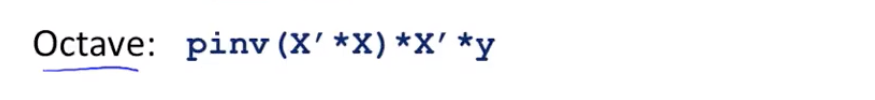
梯度下降达和正规方程法的比较

正规方程在矩阵不可逆情况下的解决办法
有些矩阵不可逆,如:奇异、退化矩阵
在octave中,pinv(伪逆),inv(逆)
使用pinv即使矩阵不可逆,也能给出正确的θ向量值。
矩阵不可逆的原因:
- 存在冗余特征——如两个人特征之间存在确定的线性关系
- 特征数量多于训练样本数量
Mar.17.2019
Octave/MATLAB教程
在Octave/MATLAB中下标从1开始
基本操作
1 | >> a = pi |
1 | >> hist(B,20) #20个柱 |
Mar.18.2019
移动数据
1 | >> load('X.txt') #载入X.txt文件 |
更多矩阵操作,略
Mar.19.2019
计算数据
- 矩阵相乘 A * B
- 矩阵元素对应相乘 A .* B
- 矩阵元素对应相加、相减、相除等
- 得到矩阵的某一部分
- 计算元素数量
- 得到逆矩阵、转置矩阵、90度旋转矩阵等
Mar.20.2019
数据绘制
基本绘制、叠加、加入图例
1 | octave:34> x = [0:0.1:10]; |
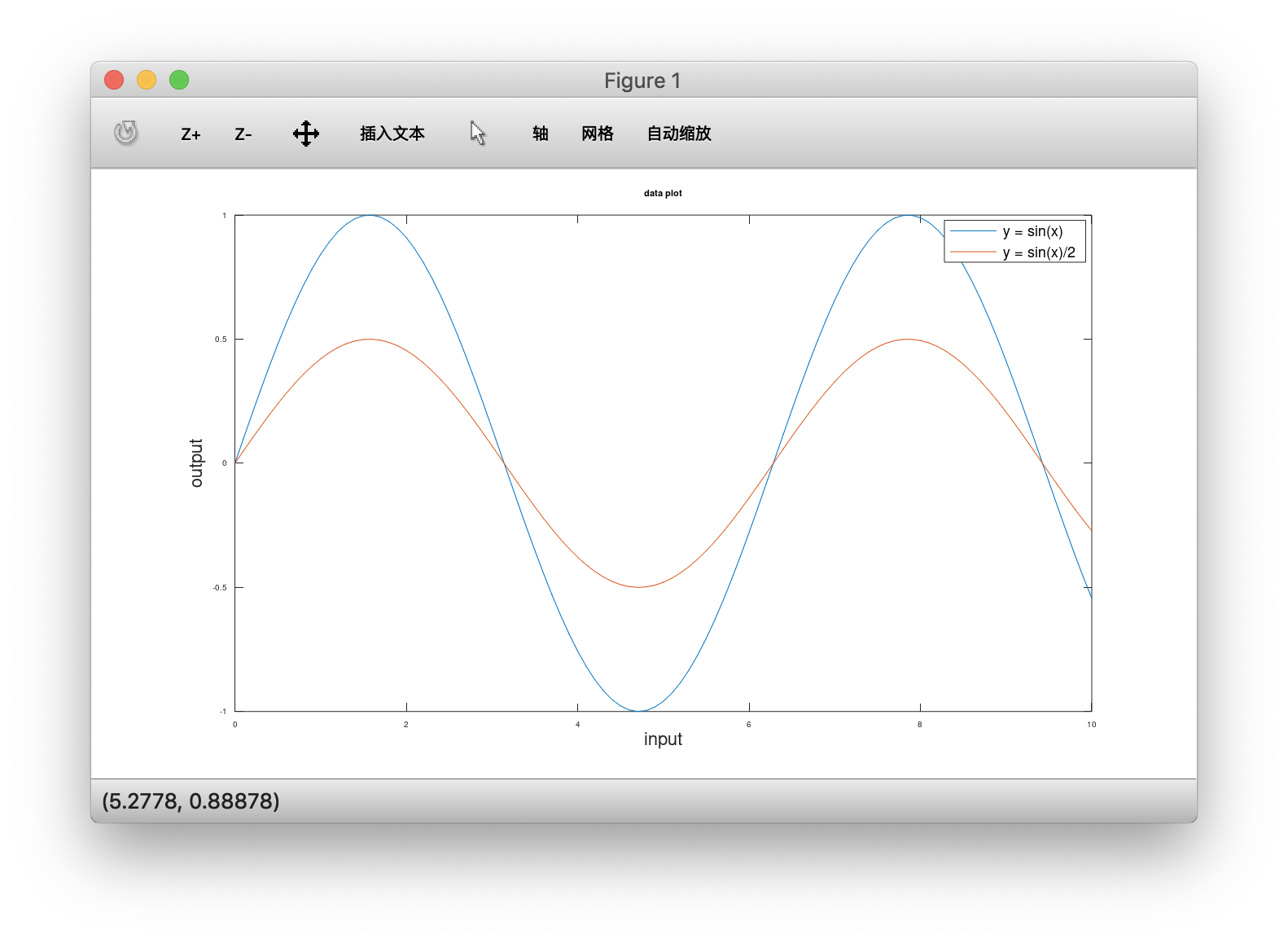
多图显示
1 | octave:45> y1 = sin(x); |
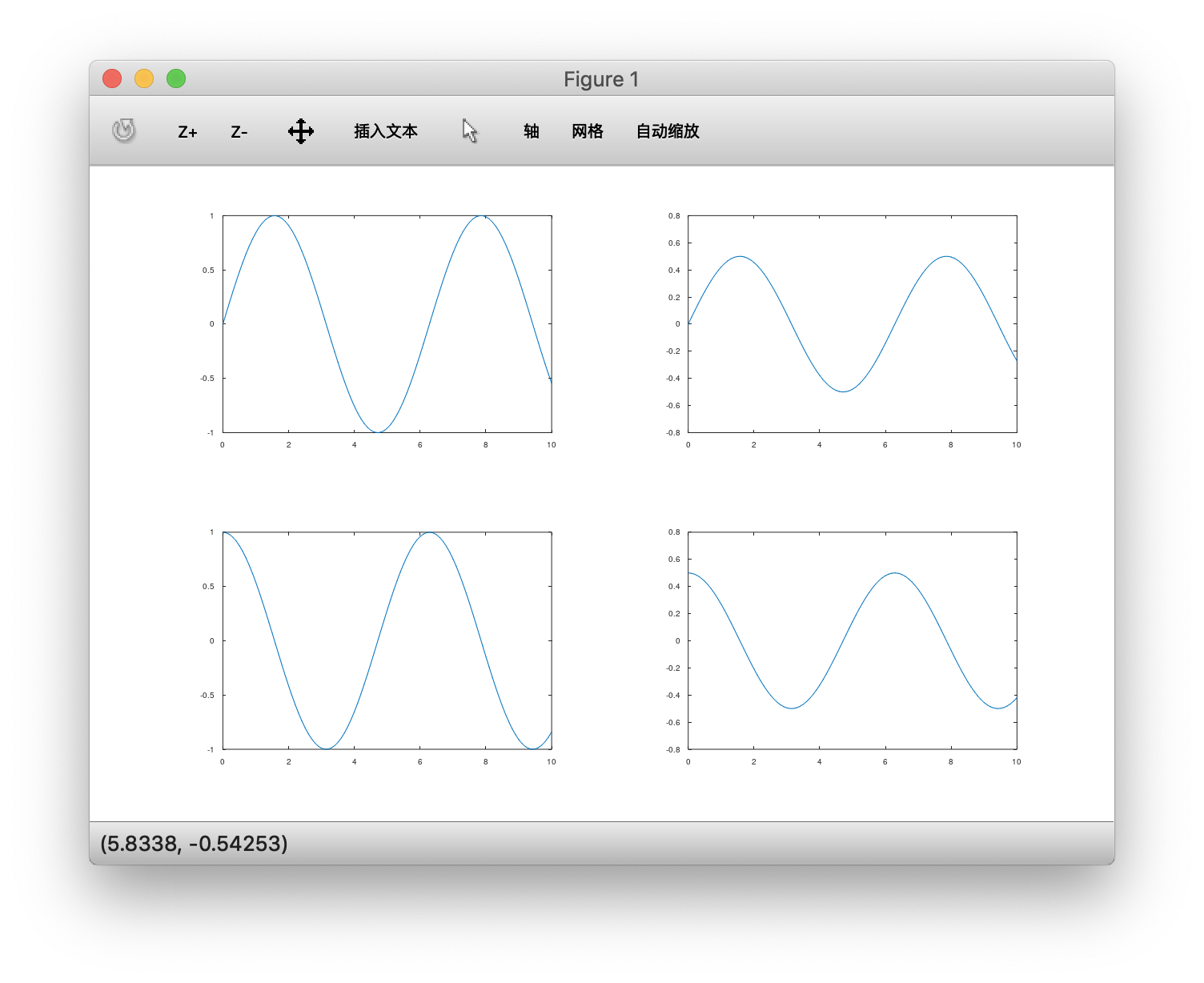
1 | > A = magic(10),imagesc(A),colorbar,colormap gray; |
Mar.23.2019
控制语句 for while if
1 | octave:7> v = zeros(1,10) |
while\break\continue 略
函数定义:
- 新建文件: function.m
文件内容:
1 | function [y1,y2] squareAndCubeThisNumber(x) |
在octave里添加这个函数文件查找路径,则在其他目录下也能直接访问该函数:1
2
3
4>> addpath('dir')
>> [a,b] = squareAndCubeThisNumber(5)
a = 25
b = 125
- 新建文件:costFunctionJ(X, y, theta)
文件内容:
1 | function j = costFunctionJ(X, y, theta) |
执行:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31>> X = [1 1; 2 2; 3 3]
X =
1 1
2 2
3 3
>> y = [1; 2; 3]
y =
1
2
3
>> theta = [0;1]
theta =
0
1
>> j = costFunctionJ(X, y, theta)
j = 0
>> theta = [0;0]
theta =
0
0
>> j = costFunctionJ(X, y, theta)
j = 2.3333
矢量(向量化vectorization)
梯度下降(costfunction为平方误差)的参数改变方程向量化:
x下标是参数编号,x上标是数据编号
向量化对代码简洁和计算加速有非常大的作用,必备操作
视频链接
编程作业
Mar.25.2019-Apr.1.2019
实验一完成和总结,包括完整代码Apr.2.2019
Logistic回归
分类
二分类:可以同样用线性回归,并设定一个阈值,比如0.5,大于判断为1,小于为0。但这是一个差劲的方法,效果不佳。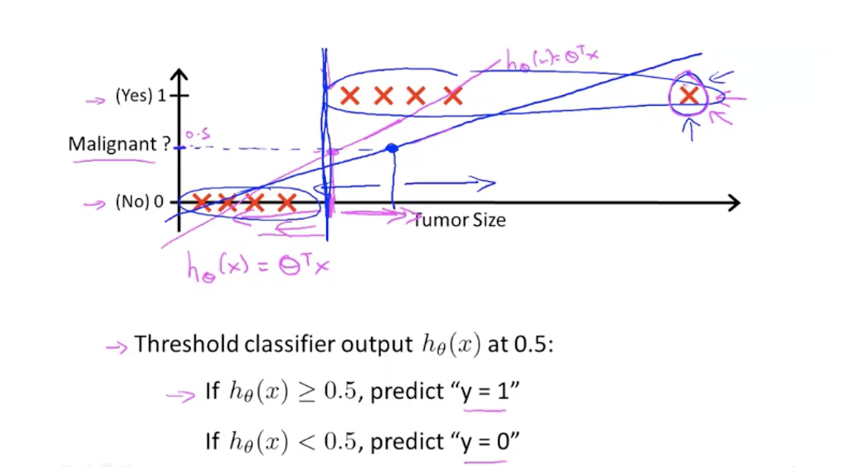
更好的方法:逻辑回归,预测值将会限定在0-1之间。
假设陈述
Sigmoid function(Logistic function)
输出值在(0,1)之间。
假设输出的值可以解释为预测值为”True“的概率
[另:几种激活函数图像]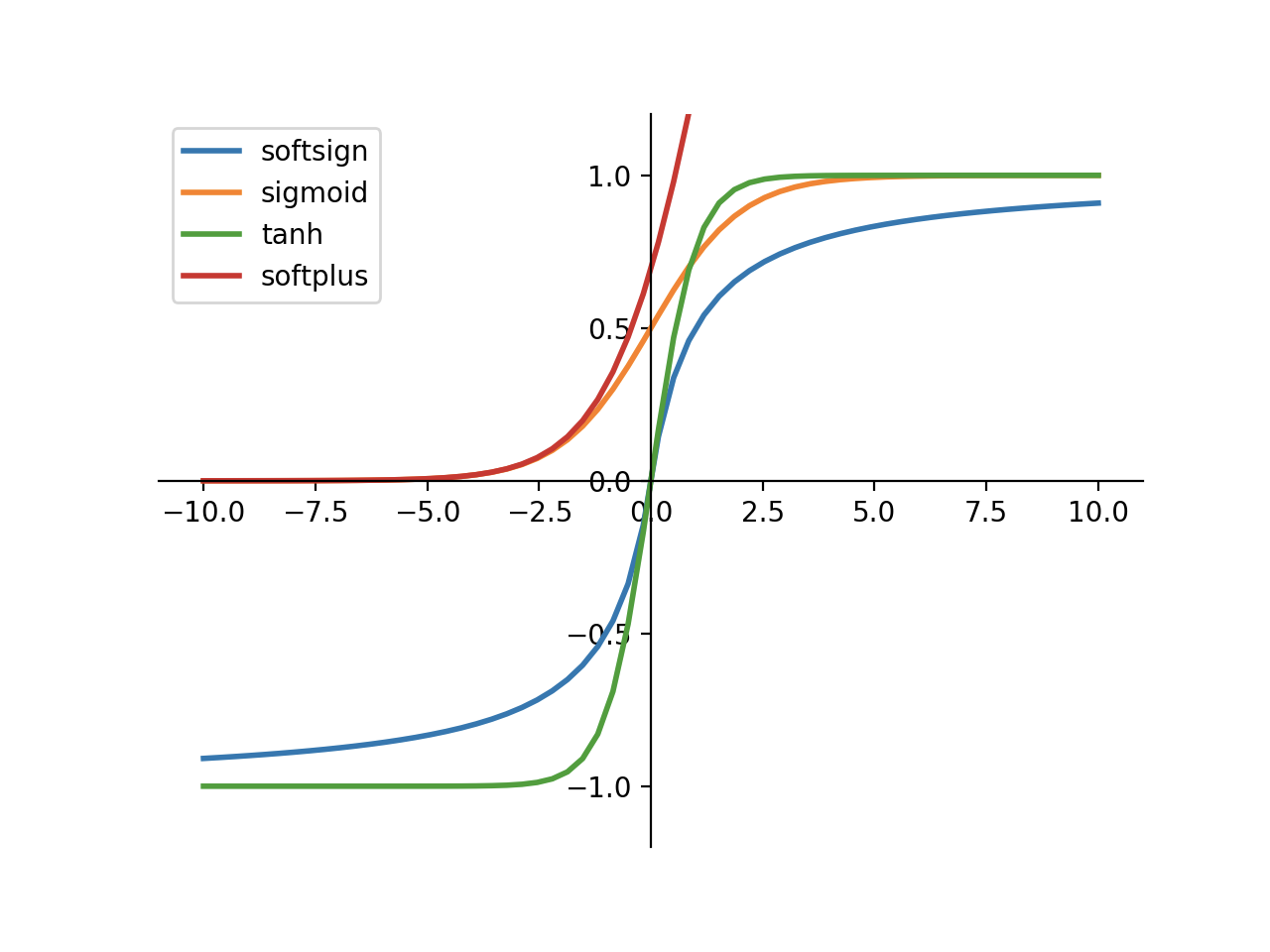
决策边界
sigmoid函数方程$f(z) = 1/(1+e^{-z})$中,当$z>0$时预测为1,当$z<0$时预测为0,我们找到一个关于θ、x的函数作为输入z,则$z=0$函数图像可以看作是一个决策边界,在它之上的,即$z>0$为类别1,在边界之下的即$z<0$为类别0。 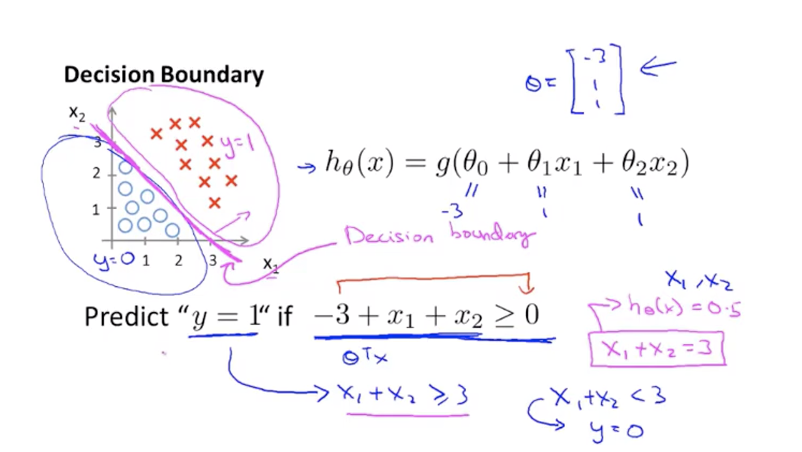

代价函数
如何选取回归模型?如何确定参数$θ$?
- 代价函数如果选取平方误差函数的话,代价函数关于参数θ的图像将会是非凸的,这样难以使用梯度下降收敛到全局最小值。
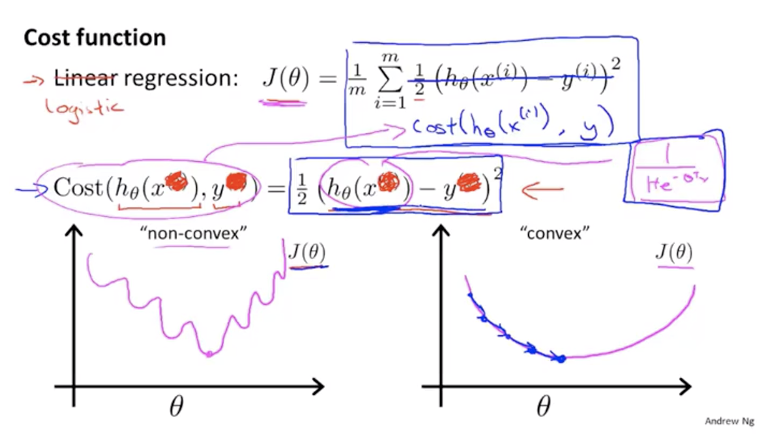
- 逻辑回归的代价函数
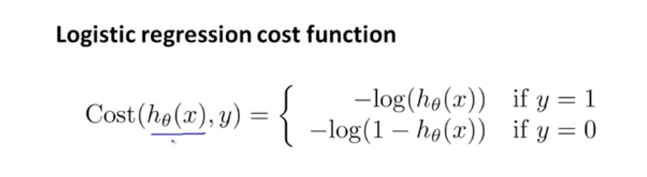
当训练数据中分类结果$y=1$时,代价函数在“预测为1的概率为0”的地方最大,即惩罚最高,在“预测为1的概率为1”的地方最小,惩罚最低。
同理当训练数据中分类结果$y=0$时,代价函数在“预测为1的概率为0”的地方最小,即惩罚最小,在“预测为1的概率为1”的地方最大,惩罚最高。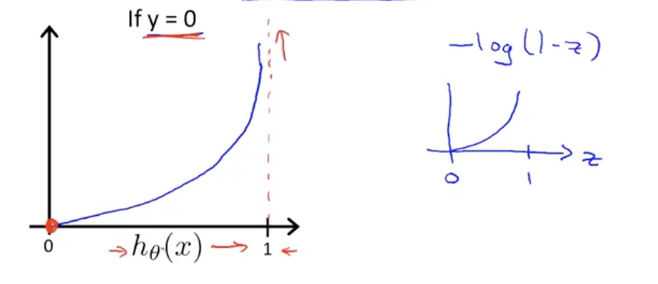
简化代价函数与梯度下降
- 整个训练集的代价函数

合并两种情况后
- 梯度下降的参数更新规则(求导)
对参数求导后的方程和线性回归中的参数更新方程相似,但其中的$h_θ(x^{(i)})$完全不同,Logistic回归中的$h_θ(x^{(i)})$经过了sigmoid函数。
Apr.3.2019
高级优化
- 一些比梯度下降更复杂的求解最优参数的算法,涉及高等数值计算,需要用的时候直接调用即可。

- 一个二维参数的例子,以及MATLAB/Octave中自动选择优化算法的具体代码。
即:先定义代价函数和代价函数关于参数$θ$的导数,使用fminunc()函数自动求解最优$θ$。
- 实际测试
costFunction.m1
2
3
4
5
6
7function [jVal, gradient] = costFunction(theta)
jVal = (theta(1)-5)^2 + (theta(2)-5)^2;
gradient = zeros(2,1);
gradient(1) = 2*(theta(1)-5);
gradient(2) = 2*(theta(2)-5);
Octave命令行中输入1
2
3
4
5
6
7
8
9
10
11
12
13
14
15>>options = optimset('GradObj', 'on', 'MaxIter', 100);
>>initialTheta = zeros(2, 1)
initialTheta =
0
0
>>[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options)
optTheta =
5
5
functionVal = 0
exitFlag = 1
找到最优参数值(5, 5),给定的函数此时值为0,即我们输入的costFunction,exitFlag表示已经收敛。
- 扩展到多维参数$θ$

多元分类:一对多
- 多元分类的实际例子

- 多元分类的一对多思想
提出一个类别作为正类,其余作为负类。
即:有n个类别,创建n个分类器,分别给出当前判断为正类的概率,最高的分类器的正类类别则为预测类别。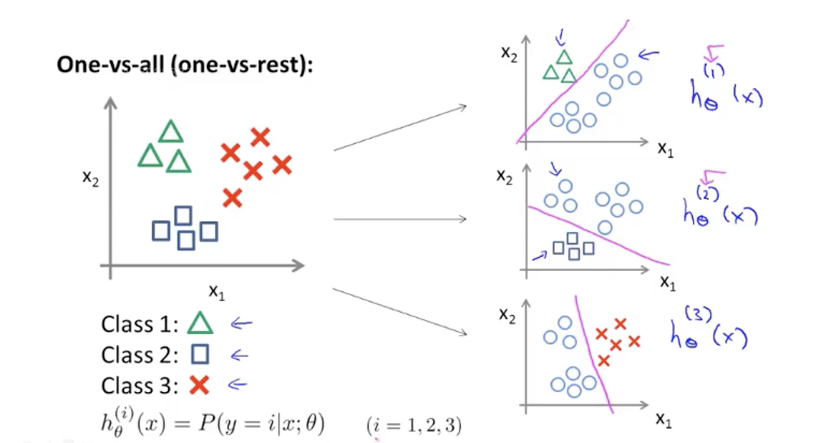
- 多元分类的一对多思想
正则化Regularization
过拟合问题Overfitting
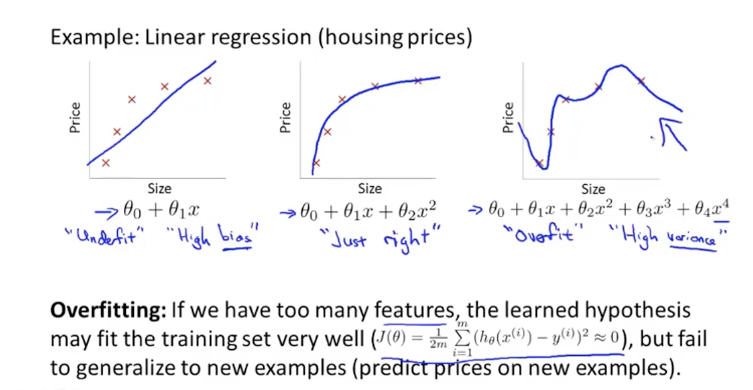
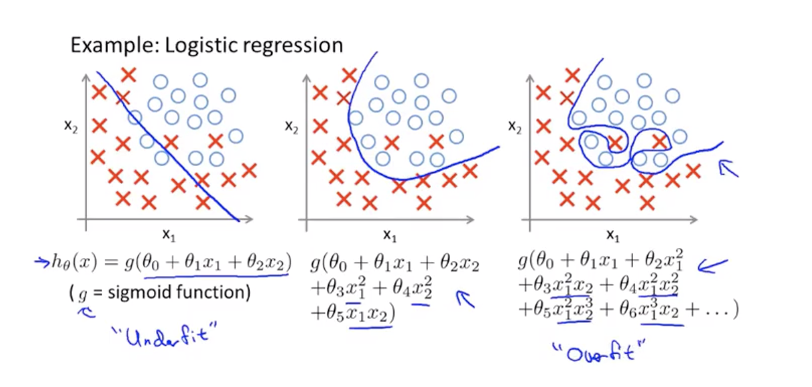
解决过拟合的方法
- 检查特征数量,减少不重要的特征
- 正则化

Apr.4.2019
costFunction
正则化
使不重要/高阶的参数$θ$尽量小,目的是
- 简化假设函数
- 减少过拟合
如何知道该缩小哪些参数$θ$?——修改costFunction,添加正则化项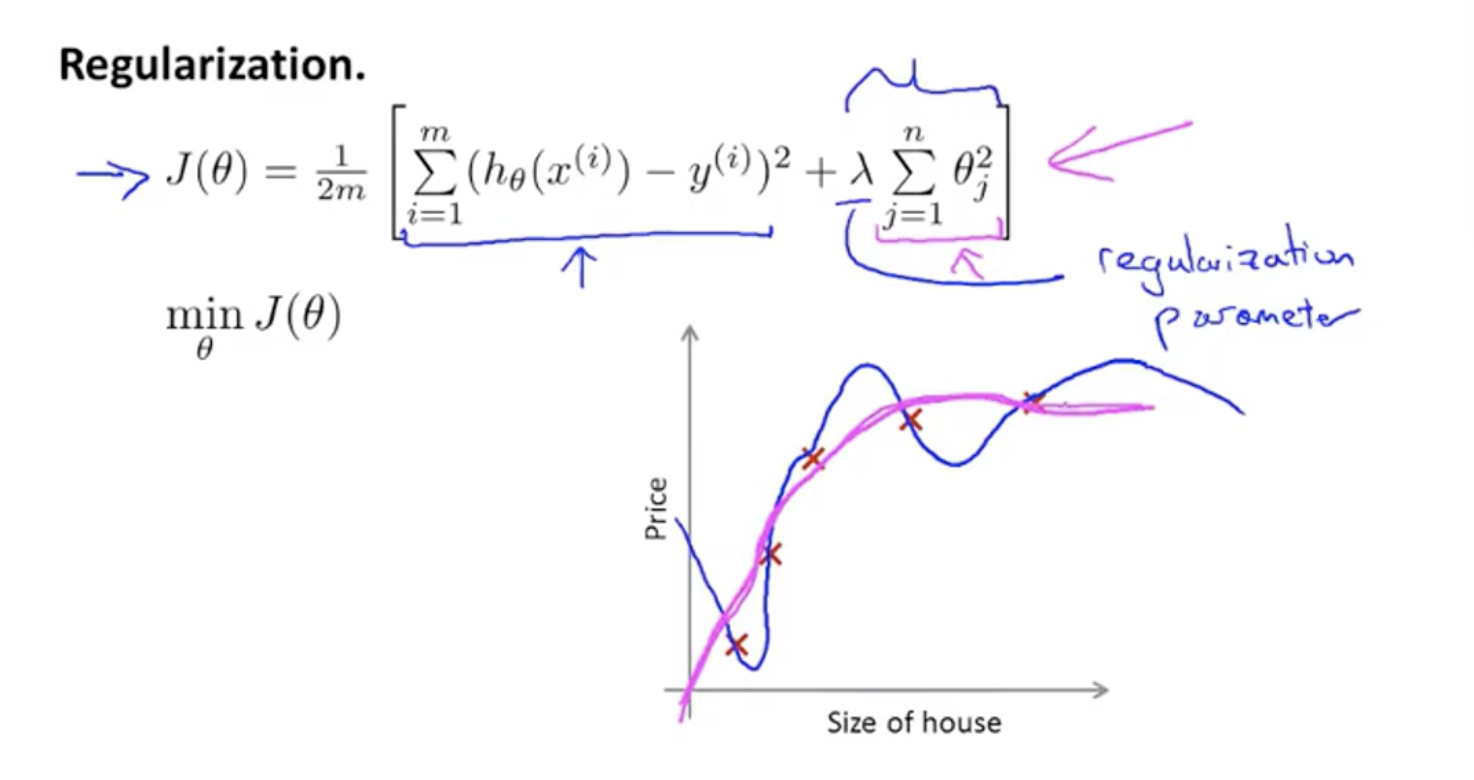
正则化参数$λ$的作用:控制两个不同目标之间的取舍(平衡),两个目标即代价函数中的两项。
在实际应用中,加上了正则化项的代价函数,确实会起到很好的效果。
线性回归的正则化costFunction
如果$λ$取值太大,则所有参数偶读趋近于零,线性回归相当于一条直线$y=θ_0$,欠拟合。
如何选择$λ$?有自动的方法。
线性回归linear regression的正则化
由正则化后的costFunction的梯度下降参数更新公式
注意到修改后的梯度下降公式与原来的公式相比可以看做是在$θ_j$上乘了一个系数$(1-α(λ/m))$
由于α很小,m很大,这个系数应该小于且接近1。
由正则化后的costFunction的正规方程求解最优参数的公式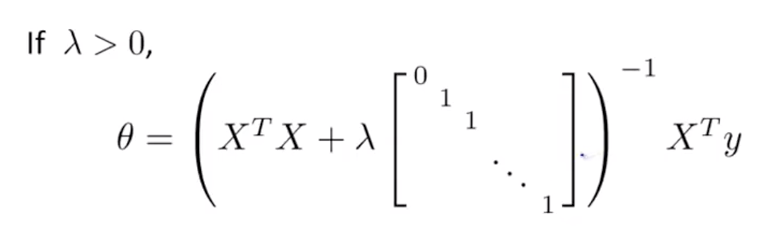
公式 $θ=(X^TX+λA)^{-1}X^Ty$
其中A为m+1 * m+1的对角线矩阵,第一个元素为0。
Apr.5.2019
Logistic回归的正则化
Logistic回归的costFunction正则化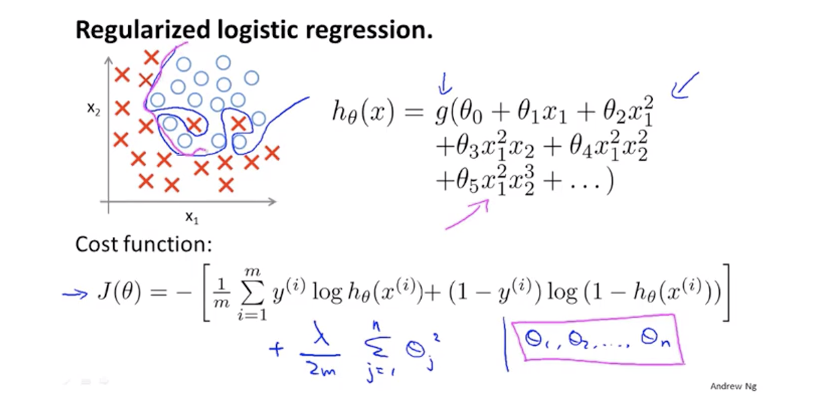
由正则化后的Logistic回归costFunction得到的梯度下降参数更新公式
看起来和线性回归的公式完全相同,但其中的$h_θ(x^{(i)})$完全不同,Logistic回归中的$h_θ(x^{(i)})$经过了sigmoid函数。
高级优化
调用高级优化函数fminunc(@costFunction,…)求解最优参数θ,其中costFunction函数需要重新编写
Apr.6.2019
神经网络
非线性假设
当假设非线性时,简单的逻辑回归算法在输入特征空间大时难以适用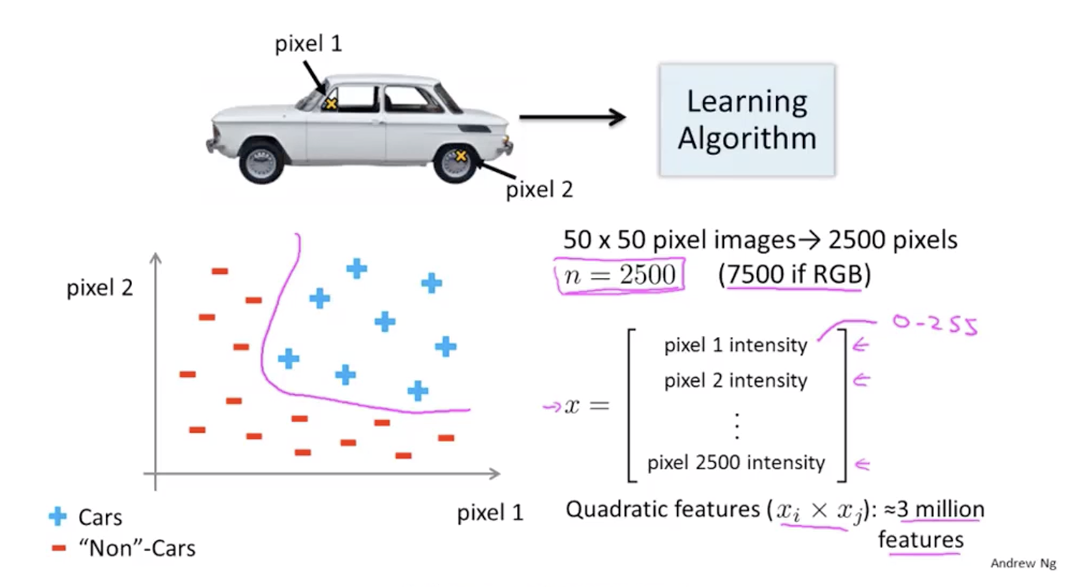
神经元与大脑
Neural Networks历史
Origins: Algorithms that try to mimic the brain.
Was very widely used in 80s and early 90s; popularity diminished in late 90s.
Recent resurgence: State-of-the-art technique for many applications.
大脑可以自主地学习并应用非常非常多不同的工作
理想:了解大脑学习的原理,并在计算机上实现,打造真正的人工智能。
对大脑的实验:通过其他感官传感器得到另一个原本由感官带来的信息(盲人通过舌头、声呐获得视觉)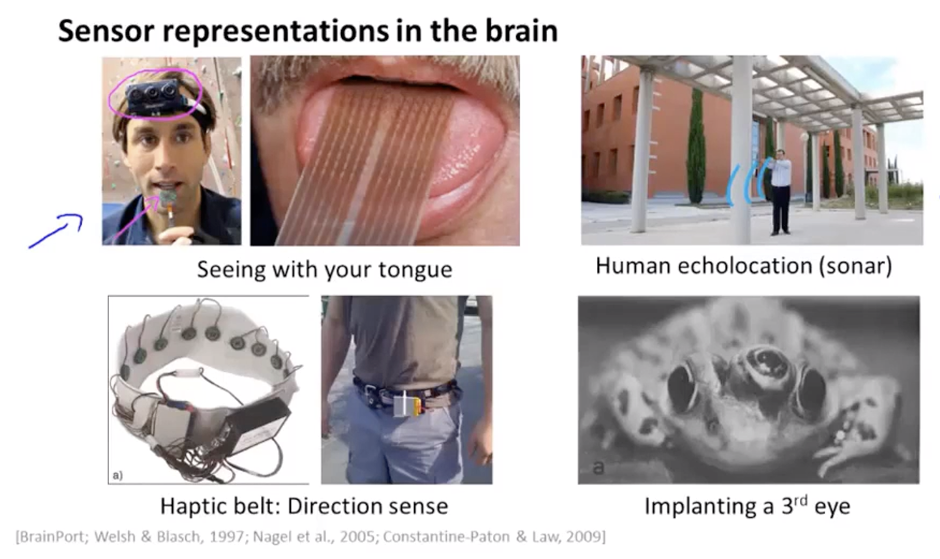
模型展示I
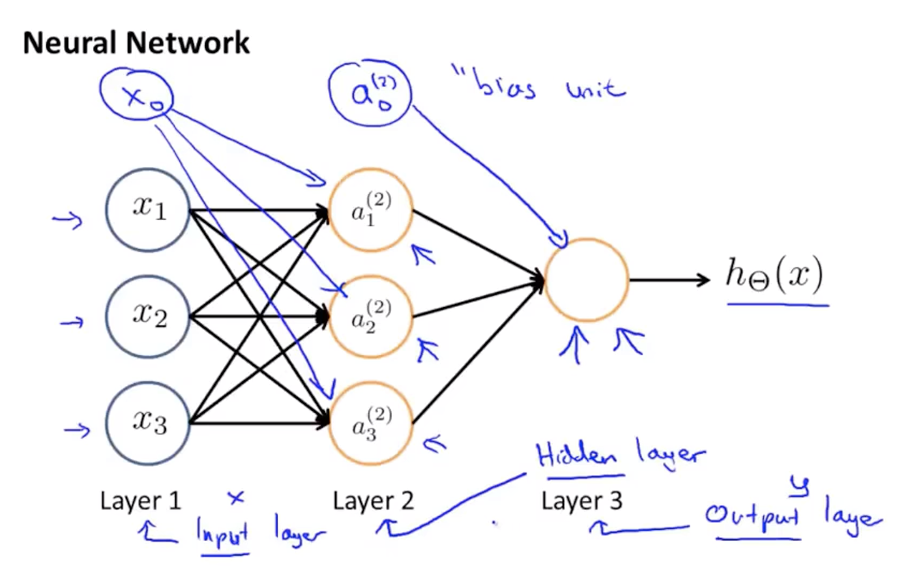
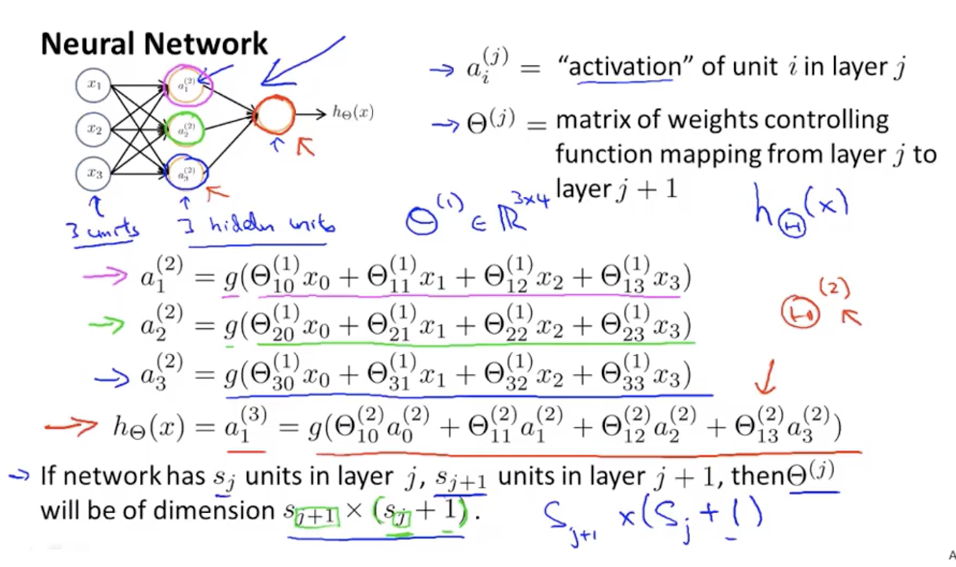
模型展示II
单隐层前馈神经网络计算具体内容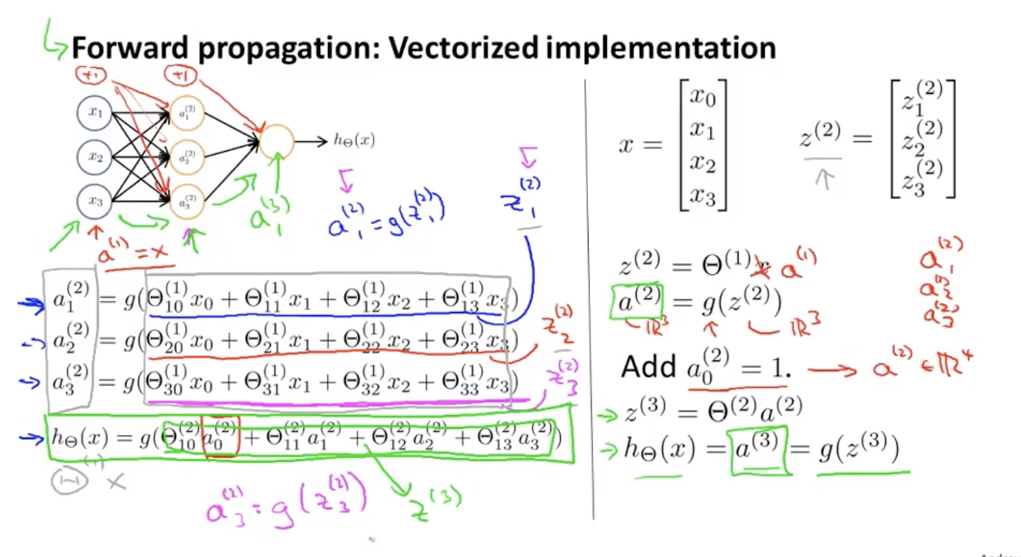
例子与直觉理解I

例子与直觉理解II
组合AND/NOTAND/OR三种结构得到表示XNOR的神经网络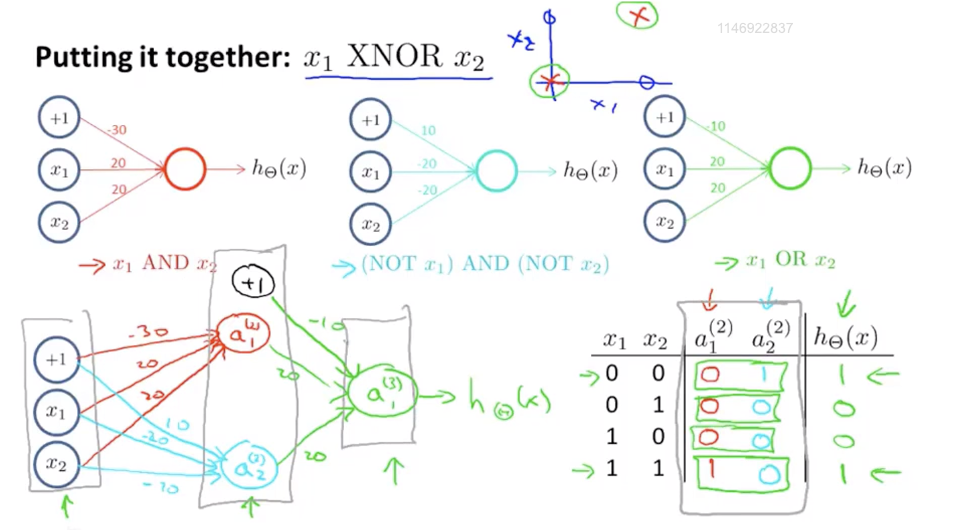
多元分类
一对多的扩展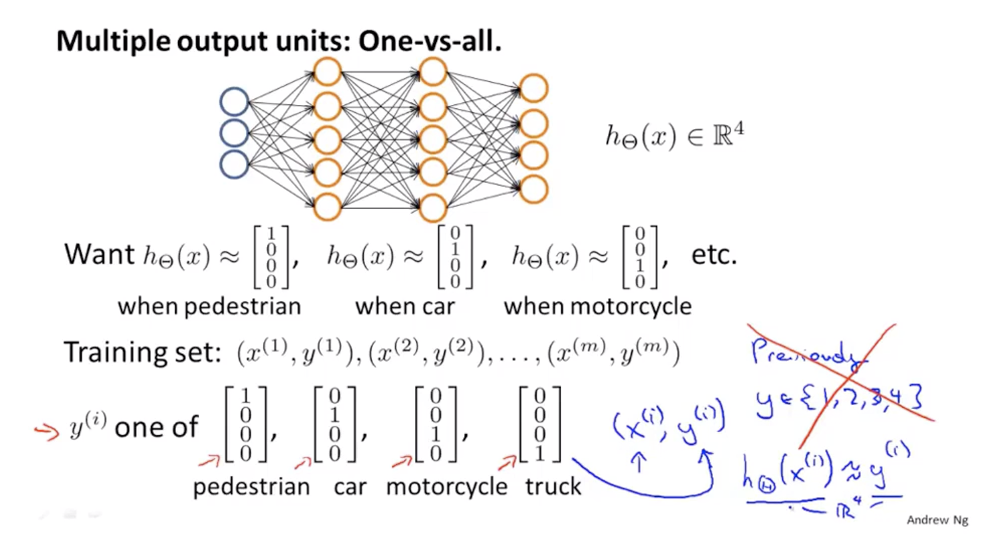
神经网络参数的反向传播算法
代价函数
(1)Logistic regression的代价函数
(2)神经网络的代价函数
其中,
反向传播算法
对于l层的元素j的“误差”是:
假设层数为4,对于每一层的输出元素来说,误差是:
其中$g^{\prime}$是激活函数的偏导数。
BP算法
训练集 $\left\{\left(x^{(1)}, y^{(1)}\right), \ldots,\left(x^{(m)}, y^{(m)}\right)\right\}$
设 $\Delta_{i j}^{(l)}=0(\text { for all } l, i, j)$
$\begin{array}{l}{\text {For } i=1 \text { to } m}\end{array}$
$\begin{array}{l}{D_{i j}^{(l)} :=\frac{1}{m} \Delta_{i j}^{(l)}+\lambda \Theta_{i j}^{(l)}} & {\text { if } j \neq 0} \\ {D_{i j}^{(l)} :=\frac{1}{m} \Delta_{i j}^{(l)}} & {\text { if } j=0}\end{array}$
其中 $\frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)=D_{i j}^{(l)}$
